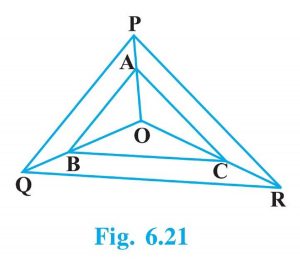
6. In Fig. 6.21, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
To prove BC || QR, we need to show corresponding angles ∠BOC & ∠OQR are equal. This is possible only when ∆OBC ~ ∆OQR. So, we need to prove that ∆OBC ~ ∆OQR.
Now as given,
∆OAB ~ ∆OPQ; So, OB/OQ = OA/OP = AB/PQ (i)
∆OAC ~ ∆OPR; So, OC/OR = OA/OP = AC/PR (ii)
In finding i and ii OA/OP is common, So:
OB/OQ = OC/OR
∠BOC = ∠OQR
Two sides in equal ratio and one same angle make two triangles similar. So,∆OBC ~ ∆OQR.
7. Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
Next: Exercise 6.3, Class 10 Maths Chapter 6, Triangles Solution.
See also: Exercise 6.1, Class 10 Maths Chapter 6 Triangles Solution.
Pages: 1 2