Theorem 6.3 NCERT Class 10 Maths Chapter 6 Triangles

Theorem 6.3 NCERT Class 10 Maths Chapter 6 Triangles

Theorem 6.3:

If the corresponding angles of the two triangles are the same, the corresponding sides are in the same ratio. So they are similar triangles. (AAA similarity)

Proof:

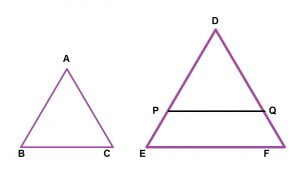
Let us illustrate using an example of the below triangle. In this figure angles in ΔABC are equal to corresponding angles in ΔDEF.

Now, let us superimpose ΔABC on ΔDEF and assume line PQ coincides BC.

Here, AB = DP and AC = DQ; and as per theorem ∠A = ∠D.

Now, as per the congruency of a triangle, if two sides of a triangle and angle between them are equal, both the triangles are congruent to each other.

So, ΔABC  ≅ ΔDPQ.

So, ∠ABC = ∠DPQ, but as given ∠ABC  = ∠DEF.

This means that  ∠DPQ = ∠DEF.

Parallel line theory: Corresponding angles of a line intersecting two parallel lines are equal.

Hence, PQ ∥ EF

Now as per theorem 6.1 (Parallel line divides the sides of the triangle in equal ratio)

DP/PE = DQ/DF.

Hence, AB/DE = BC/EF = AC/DF.

Next: Theorem 6.4.

See also: Theorem 6.2: If a line dives the two sides of the triangle in equal ratio, the line is parallel to the third side of the triangle.

Ref: Chapter 6

Theorem 6.3 NCERT Class 10 Maths Chapter 6 Triangles