Triangles Activity Solution

Triangles Activity Solution Chapter 6 Class 10 Mathematics

Chapter 6 Activity 1

Activity 1 asks us to observe the sides and angles of the polygon formed in the picture.

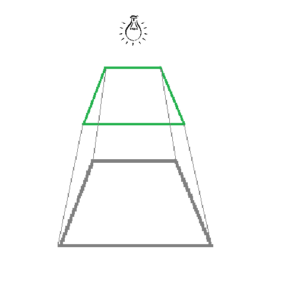
Observation:

Corresponding angles of the polygon are of the same value and their sides are in equal ratio.

Explanation:

Light travels in a straight direction. Here the real polygon blocks the light. It results in the formation of a shadow. Since the source of light is at the center the shadow is proportional to the actual polygon.

Activity 2

An angle is givens  and it says that

In ∠XAY

AP = PQ= QD = DR = RB

&

DE // BC

Now it asks us for AD/AB and AE/EC

Observation:

AE/EC and DE/BC are equal.

Explanation:

∠ A is common, ∠ ADE and ∠ ABC are corresponding angles of a line 

Here the triangles are similar. As a result, ratios of their corresponding sides are equal.

for proof see theorem 6.1

Activity 3

Activity 3 is the inverse of activity 2. It says that if we draw lines that are equal in ration then lines are parallel.

Activity 4

Activity 4 asks us to draw two triangles of different sizes but with the same angles.

Observation:

The ratio of their sides is the same.

Explanation:

This is AAA similarity. When all angles of triangles are the same as the angles of a corresponding triangle, their sides are in the same ration. Ref: Theorem 6.3

Activity 5

Activity 5 is the converse of activity 4. It says that when the corresponding ratio of sides is equal to each other then both have the same corresponding angles. Theorem 6.4

Activity 6

Activity 6 says that if the ratio of two sides of a triangle and the angle between the two sides are equal then triangles are similar. SAS See Theorem 6.5.

Triangles Activity Solution Chapter 6 Class 10 Mathematics