Proofs in Mathematics A1 Class 10 Exercise Solution

Proofs in Mathematics A1 Class 10 Exercise Solution

EXERCISE A1.1 Page 316

1. State whether the following statements are always true, always false or ambiguous. Justify your answers.

(i) All mathematics textbooks are interesting.
(ii) The distance from the Earth to the Sun is approximately 1.5 × 108 km.
(iii) All human beings grow old.
(iv) The journey from Uttarkashi to Harsil is tiring.
(v) The woman saw an elephant through a pair of binoculars.

Answer: (i) Ambiguous: It may vary from person to person. One may find a book interesting, while another person may be repealed by the same book.

(ii)Always rue: The distance between the earth and the moon as estimated by the scientists is around 149.86 million years i.e. approx 1.5 x 108.

(iii)Always true: We all see people grow and become old. A child becomes a boy; then a teen; then an adult and then into an old person.

(iv)Ambiguous: You may feel tired if you go on foot. However, if you go by a chopper it won’t be tiresome.

(v)Ambiguous: Here we do not know which woman the book is referring to.

2. State whether the following statements are true or false. Justify your answers.

(i) All hexagons are polygons. (ii) Some polygons are pentagons.
(iii) Not all even numbers are divisible by 2. (iv) Some real numbers are irrational.
(v) Not all real numbers are rational.

Answer: (i) True: A two-dimensional closed structure made by 3 or more lines is a polygon. So, a hexagon is also a polygon.

(ii) True: Some polygons may have 5 straight lines making it a pentagon.

(iii)False: We call a number as even if it is divisible by two.

(iv)True: Rational numbers (simple fractions) are those which can be put into p/q form where p and q are integers. Real numbers may be rational or irrational. So, some real numbers may be irrational while some may be rational.

(v)True: See above.

3. Let a and b be real numbers such that ab ≠ 0. Then which of the following statements are
true? Justify your answers.

(i) Both a and b must be zero. (ii) Both a and b must be non-zero. (iii) Either a or b must be non-zero.

Answer: (ii) ab ≠ 0 is possible only if both a and b are non-zero numbers.

4. Restate the following statements with appropriate conditions, so that they become true.

(i) If a²> b², then a > b. (ii) If x²= y², then x = y. (iii) If (x + y)² = x²+ y², then x = 0. (iv) The diagonals of a quadrilateral bisect each other.

Answer: (i)possible if a and b are positive numbers. (square of a negative number is a positive number. So if we take a in negative and b as positive second equation will fail.)

(ii) Here it is possible only if either both numbers are negative or both are positive.

(iii) here, both equations are true only if y is either 0 or 1.

(iv) Only the diagonals of a parallelogram (rhombus/square/rectangle) bisect each other. So to make the statement always true, we will have to specify that the quadrilateral is a parallelogram.

EXERCISE A1.2 Page 318

1. Given that all women are mortal, and suppose that A is a woman, what can we conclude about A?

Answer: From both the statements we can conclude that A is a woman and is mortal.
2. Given that the product of two rational numbers is rational, and suppose a and b are rationals, what can you conclude about ab?

Ans: ab is also a rational number.
3. Given that the decimal expansion of irrational numbers is non-terminating, non-recurring, and √17 is irrational, what can we conclude about the decimal expansion of √17?

Answer: The decimal expansion of √17 also will be non-terminating and non-recurring.
4. Given that y = x² + 6 and x = – 1, what can we conclude about the value of y?

Answer: From both the condition we can find that the value of y is 7.
5. Given that ABCD is a parallelogram and ∠ B = 80°. What can you conclude about the other angles of the parallelogram?

Answer: Opposite angles of a parallelogram is equal. So if ∠ B = 80° then ∠ D = 80°, ∠ A = 100°  and ∠ C = 100°.

6. Given that PQRS is a cyclic quadrilateral and also its diagonals bisect each other. What can you conclude about the quadrilateral?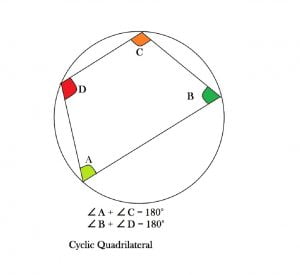

Answer: The quadrilateral is a rectangle. Explanation: Sum of opposite angles of a Cyclic quadrilateral is 180° and opposite angles of a parallelogram are equal ( diagonals of a parallelogram bisect each other). So each angle of the quadrilateral is  90°.

7. Given that √p is irrational for all primes p and also suppose that 3721 is a prime. Can you conclude that 3721 is an irrational number? Is your conclusion correct? Why or why not?

Answer: From both the statements we can say that the square root of 3721 is irrational.

This conclusion is incorrect because 3721 is not a prime number as it is square of 61 i.e. 61×61=3721. Here our statement was false. As a result, we came with the wrong conclusion.

EXERCISE A1.3 Page 323

In each of the following questions, we ask you to prove a statement. List all the steps in each proof, and give the reason for each step.

1. Prove that the sum of two consecutive odd numbers is divisible by 4.

Proof:

The formula of an odd number is 2n+1 (General property of integer)

then the sum of its consecutive odd number will be: (2n+1)+(2n+3)

=4n+4

=4(n+1)

Hence, it will be divisible by 4.

 

2. Take two consecutive odd numbers. Find the sum of their squares, and then add 6 to the result. Prove that the new number is always divisible by 8.

Answer: Odd number = 2n+1 (General property of integer)

Next consecutive odd no= 2n+3 (General property of integer)

As per question

(2n+1)² + (2n+3)²+6

= (4n²+1+4n) + (4n²+9+12n +6  (From Algebraic formula (a+b)² = (a²+b²+2ab) )

=8n+16+16n

=8(n²+2+2n)

Hence the new number formed as per the question is divisible by 8.

3. If p ≥ 5 is a prime number, show that p²+ 2 is divisible by 3.

Proof:  Let the prime number is ‘p’

Dividing p by 6, possible forms are 6k, 6k + 1, 6k + 2, 6k + 3, 6k + 4, or 6k + 5, where k is an integer. (Euclid’s division formula)

Here the number is prime so only 6k + 1 or 6k + 5 form is possible.

Now we will prove each case seperately.

Case 1: p as 6k + 1

as per the question

p²+ 2 = (6k + 1)²+2

=36k²+1+12k+2

= 36k²+3+12k

=3(12k²+1+4k)

Hence divisible by 3.

Case 2: p as 6k +5

p²+ 2 = (6k + 5)²+2

=36k²+25+60k+2

= 36k²+27+60k

=3(12k²+9+20k)

Hence divisible by 3.

4. Let x and y be rational numbers. Show that xy is a rational number.

Proof: x and y are the rational numbers. So, they can be expressed as fraction of integer.

Let x =m/n and y =p/q where n and q  are non-zero integers.

Now, as per the question,

xy = m/n X p/q

=mp/nq

here mp and nq will be an integer. ( By the general property of integer)

and nq will not be equal to zero. ( By the general property of integer)

Hence, Proved

5. If a and b are positive integers, then you know that a = bq + r, 0 ≤ r < b, where q is a whole number. Prove that HCF (a, b) = HCF (b, r).
[Hint : Let HCF (b, r) = h. So, b = k1
h and r = k2
h, where k1
and k2
are coprime.] 6. A line parallel to side BC of a triangle ABC, intersects AB and AC at D and E respectively. Prove that
AD/DB =AE/EC

 

Ref: NCERT Class 10 Mathematics chapter 1.